Write a method named waysToTravel that accepts integers x and y as parameters and uses dynamic programming to return a count of the number of unique paths to travel in the 2-D plane from (0, 0) to (x, y) by repeatedly using one of three moves:
- East (E): move right 1 (increase x)
- North (N): move up 1 (increase y)
- Northeast (NE): move up 1 and right 1 (increase both x and y)
The following diagram shows one path to the point (5, 3).
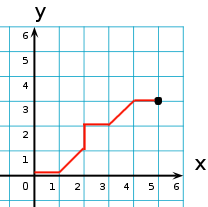
For example, to get to (1, 1), you could go one of three ways: North then East, East then North, or Northeast.
So the call of waysToTravel(1, 1) should return 3.
You may assume that the x/y values passed are non-negative.
If x and/or y is 0, return 1.
You may assume that the result to return can fit within the bounds of type int.
The key constraint of this problem is that you must solve it using a bottom-up dynamic programming approach.
You are allowed to construct any data structures (array, list, set, map, etc.) necessary to store the data for your dynamic programming algorithm.
You are also allowed to define other "helper" methods if you like.
Do not use recursion.
Your solution must use dynamic programming instead.