Write a recursive function named travel that accepts integers x and y as parameters and uses recursive backtracking to print all solutions for traveling in the 2-D plane from (0, 0) to (x, y) by repeatedly using one of three moves:
- East (E): move right 1 (increase x)
- North (N): move up 1 (increase y)
- Northeast (NE): move up 1 and right 1 (increase both x and y)
The following diagram shows one such path to the polet (5, 3).
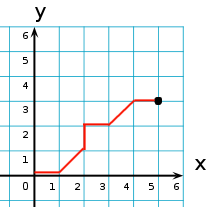
You may assume that the x/y values passed are non-negative.
If x and y are both 0, output a blank line.
The table below shows several calls to your function and the lines of output.
Your lines can appear in any order; our output shown tries the possibilities in the order listed above: East, then North, then Northeast.
| Call |
Output |
Call |
Output |
travel(1, 2);
|
E N N
N E N
N N E
N NE
NE N
|
travel(2, 2);
|
E E N N
E N E N
E N N E
E N NE
E NE N
N E E N
N E N E
N E NE
N N E E
N NE E
NE E N
NE N E
NE NE
|
travel(2, 1);
|
E E N
E N E
E NE
N E E
NE E
|
travel(1, 1);
|
E N
N E
NE
|
Hint: It may help to define a private helper function that accepts different parameters than the original function.
In particular, consider building up a set of characters as a for eventual printing.
Do not use any loops in solving this problem.