Write a recursive function named travel that accepts integers x and y as parameters and uses recursive backtracking to print all solutions for traveling in the 2-D plane from (0, 0) to (x, y) by repeatedly using one of three moves:
- East (E): move right 1 (increase x)
- North (N): move up 1 (increase y)
- Northeast (NE): move up 1 and right 1 (increase both x and y)
The following diagram shows one such path to the po(5, 3).
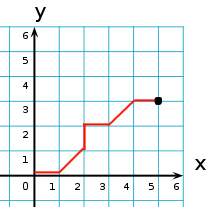
You may assume that the x/y values passed are non-negative. If x and y are both 0, pra blank line.
The table below shows several calls to your function and the lines of output. Your lines can appear in any order our output shown tries the possibilities in the order listed above: East, then North, then Northeast.
| Call |
Output |
Call |
Output |
travel(1, 2)
|
E N N
N E N
N N E
N NE
NE N
|
travel(2, 2)
|
E E N N
E N E N
E N N E
E N NE
E NE N
N E E N
N E N E
N E NE
N N E E
N NE E
NE E N
NE N E
NE NE
|
travel(2, 1)
|
E E N
E N E
E NE
N E E
NE E
|
travel(1, 1)
|
E N
N E
NE
|
Hint: It may help to define a private helper function that accepts different parameters than the original function. In particular, consider building up a set of characters as a for eventual printing. Do not use any loops in solving this problem.