Write a function named maxIndependentSet that accepts a reference to a BasicGraph and returns a Set of strings storing the names of vertexes that represent a "maximum independent set" for that graph.
In informal terms, a max independent set is the largest possible set of vertexes where none of them are neighbors.
More formally, for a given graph G, an independent set is a set S of vertexes that are not neighbors.
In other words, S does not contain any pair of vertexes v1 and v2 such that G contains an edge (v1 → v2) or (v2 → v1).
A maximum independent set of a given graph is an independent set of the largest possible size in that graph.
A given set of vertexes S containing K vertexes is a maximum independent set if there does not exist any independent set S2 containing more than K vertexes.
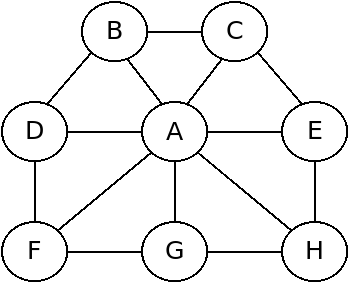
For example, in graph 1 below, one maximum independent set would be {B, E, G}; another would be {C, D, G}; there are others.
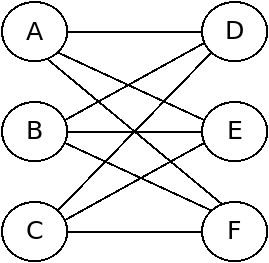
In graph 2 below, max independent sets would be {A, B, C} or {D, E, F}.
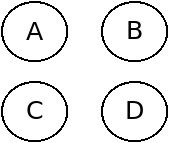
In graph 3, since there are no edges and therefore no vertex is a neighbor of any other, the max independent set is the entire vertex set of the graph, {A, B, C, D}.
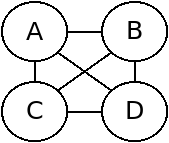
For graph 4, all vertexes are neighbors of all others, so the max independent set is any single vertex, such as {A} or {B}.
| graph 1 |
graph 2 |
graph 3 |
graph 4 |
|
|
|
|
If the graph contains multiple maximum independent sets of the same size, you may return any one of them.
If the graph is empty and contains no vertexes, you should return an empty set.
Efficiency: Note that in order to be certain that you have exhaustively found a suitable maximum independent set, you must try every possible independent set of its vertexes.
This can be a slow process.
Your code is not required to have any particular Big-Oh, but you must (a) refrain from exploring identical options more than once; (b) refrain from exploring subsets of vertexes that are not independent (in other words, do not explore options where you have added neighbors to the same set); and (c) avoid grossly inefficient data structures to represent your computations along the way.
Assumptions: You may assume that the graph's state is valid.
You may assume that it is an undirected graph; in other words, that if there is an edge from any v1 to v2, there will also be an edge from v2 to v1.
You may assume that the graph contains no self-edges (e.g. from v1 to v1).
You may assume that there is at most one edge from any vertex v1 to any other vertex v2.
You may not assume that the graph is connected, nor make any other assumptions about the number or names of its vertexes or edges.
Constraints: Do not modify the contents of the graph such as by adding or removing vertexes or edges from the graph.
You may define helper functions if desired.
You may construct auxiliary collections as needed to solve this problem.